Di Nicole Zhu.

Recentemente ho ascoltato questo podcast ZKFM, che ha fornito esempi pratici per spiegare in modo chiaro concetti chiave di zero-knowledge. Mi sono sentita ispirata a trascriverli qui.

Nella crittografia, le prove zero-knowledge ti permettono di convincermi che sai qualcosa, o hai fatto qualcosa, senza rivelarmi quale è la tua cosa segreta.

L’importanza della zero-knowledge consiste nel garantire privacy in situazioni in cui altrimenti dovresti rivelare informazioni riservate. Gli esempi includono:

• Accesso a un sito web: anziché digitare la password in un sito web potenzialmente pericoloso, è sufficiente inviare una prova che “conosci la tua password”.
• Verifica di identità: anziché fornire il cognome da nubile di tua madre al telefono, a uno sconosciuto agente di call center bancario, puoi semplicemente inviare una prova (un fingerprint crittografico) che tu sei chi dici di essere.
• Invio di transazioni private su blockchain: invece di inviare denaro su Bitcoin, dove il tuo ledger finanziario è pubblico, puoi inviare una prova che il tuo denaro è valido (non c’è doppia spesa) senza rivelare i tuoi balance, come reso popolare da ZCash.

Esempio 1: Dimostra di sapere dove si trova Waldo, senza condividere la sua posizione

In questo esempio, Alice e Bob stanno competendo per trovare Waldo in una famosa serie di libri per bambini. Lo scopo è quello di individuare Waldo in un mare di forme che assomigliano a lui.

Il rompicapo:

Alice: So dov’è Waldo!

Bob: Alice, sai cos’è un bugiardo?

Alice: Posso dimostrarti dove è senza rivelare la sua posizione.

Per difendere la sua moralità, Alice escogita due soluzioni per dimostrare quello che sa.

Prova 1

Alice ritaglia Waldo dalla sua scena e mostra a Bob solo il frammento di Waldo. Per garantire che Alice non abbia semplicemente stampato una nuova immagine di Waldo, Bob può filigranare la parte posteriore della pagina di scena di Alice. In alternativa, può compiere una completa perquisizione su Alice prima che Alice entri in una stanza segreta per tagliare la pagina.

Prova 2

Alice fa un buco in un foglio di cartone molto grande e opaco. Posiziona il ritaglio di cartone sulla scena originale. In questa soluzione, viene mostrato solo Waldo. Le sue coordinate in relazione al resto della scena sono ancora sconosciute. Più tardi, Alice può riprodurre la scena sottostante per dimostrare che ha usato il puzzle originale.

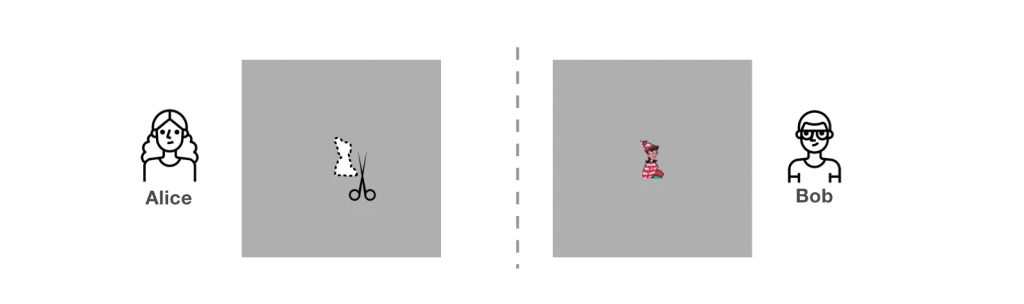
Validità, completezza e Zero-knowledge

Entrambe le soluzioni soddisfano le tre importanti proprietà dei sistemi di prova Zero-knowledge: validità, completezza e zero-knowledge.

Alice è in grado di utilizzare le stesse prove per verificare di aver trovato Waldo molte volte a partita e in molti giochi. In questo senso, i suoi sistemi di prova ottengono statistiche:

1. Validità – tutto ciò che è dimostrabile è vero: supponendo che Alice non conosca le posizioni di Waldo e presenti pezzi casuali della scena ai suoi sistemi di prova… quindi, i suoi fori di cartone mostreranno immagini casuali senza Waldo. In parole povere, i sistemi di prova di Alice sono attendibili e non le permettono di barare.
2. Completezza – tutto ciò che è vero ha una prova: finché Alice trova Waldo, è in grado di usare costantemente le sue prove per mostrare Waldo, in ogni gioco. In parole povere, i sistemi di prova di Alice convincono Bob sul fatto che lei abbia trovato Waldo.
3. Zero-Knowledge – viene rivelata solo la dichiarazione che viene dimostrata: mentre Alice dimostra a Bob di aver trovato Waldo, l’unica informazione rivelata a Bob è che “Alice ha trovato Waldo”. La posizione di Waldo non viene mai rivelata. In parole povere, i sistemi di prova di Alice dimostrano la sua vittoria a Bob, senza rivelare le sue informazioni.

Esempio 2: una prova zero-knowledge interattiva

Quello che segue è un esempio di prova zero-knowledge interattiva. In questo esempio, Alice è daltonica mentre Bob non lo è. Non crede all’affermazione di Bob di poter vedere i colori.

In qualità di crittografa intelligente che è, Alice procura due palline (una rossa e una blu) e concepisce una prova interattiva per Bob, usando un meccanismo di sfida e risposta.

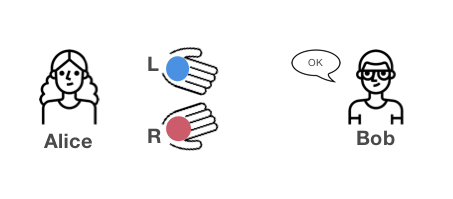
Alice: Sto tenendo una palla rossa e una palla blu. Ora metto le mani dietro la mia schiena, quindi non puoi vedere. Durante questo periodo, posso o non posso scambiare le palle tra le mie mani. Successivamente, ti mostrerò di nuovo le palle.

Bob: Ok, quindi vuoi che ti dica se hai cambiato le palle o no.

Alice: Corretto, solo qualcuno che può vedere il colore sarà in grado di dirmi regolarmente quello che ho fatto.

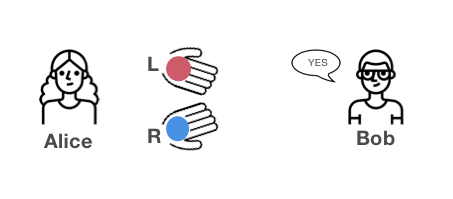
Alice: Ho mescolato le palle?

Bob: Sì, le palle sono in mani diverse.

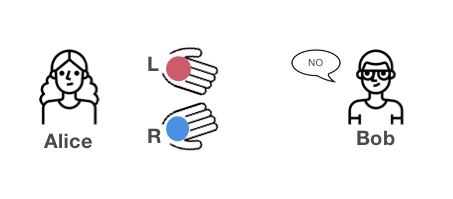
Alice: Ho mescolato le palle?

Bob: No, le palle sono nelle stesse mani.

In questa dimostrazione, Alice e Bob ripeteranno questo gioco molte volte finché Alice non sarà convinta. Venti giochi dopo, Alice è convinta che c’è solo una possibilità su 1.048.576 che Bob abbia avuto fortuna in ogni singolo tentativo. È ragionevolmente convinta che Bob possa vedere il colore.

Questo esempio di sfida-risposta indica che i sistemi di prova zero-knowledge sono solo garanzie statistiche della possibilità che qualcosa si sia verificato.

Esempio 3: Prova zero-knowledge non interattiva

Di seguito è riportato un esempio di prova zero-knowledge non interattiva, che non richiede la precedente dinamica sfida-risposta tra Alice e Bob. In questo caso, Alice può generare tutte le sfide contemporaneamente, e in seguito Bob può rispondere in un secondo momento. Tali prove non interattive consentono a molte parti di verificare le affermazioni di Alice, non solo a Bob.

Il rompicapo:

Alice vuole dimostrare a Bob e al suo altezzoso club di Sudoku di aver risolto un indovinello di Sudoku che loro non sono stati in grado di risolvere.

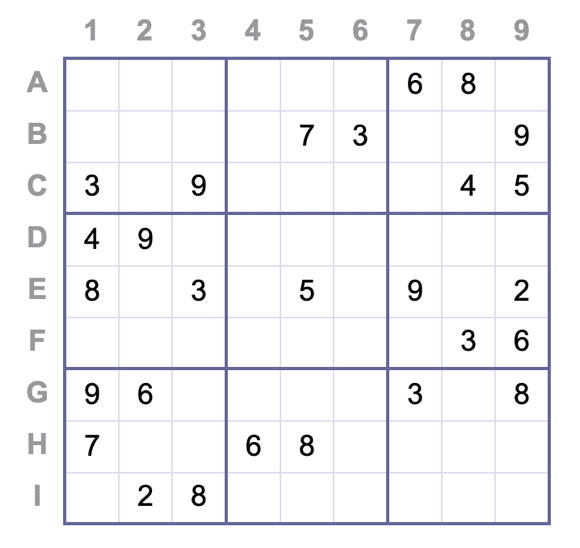
(Ogni cella deve contenere un numero (1-9) che è unico per la riga, la colonna e la griglia 3×3)

Per fare ciò, Alice sviluppa una macchina a prova di manomissione che fornisce la prova a Bob e agli amici. La macchina di Alice segue uno specifico protocollo, pubblicamente verificabile, con la seguente logica.

1) Innanzitutto, Alice riproduce nella macchina il puzzle originale non risolto. Per ciascuna cella con un valore esistente, essa posiziona automaticamente tre carte scoperte con il numero corrispondente, ad es. la cella C3 ha tre carte numero 9;

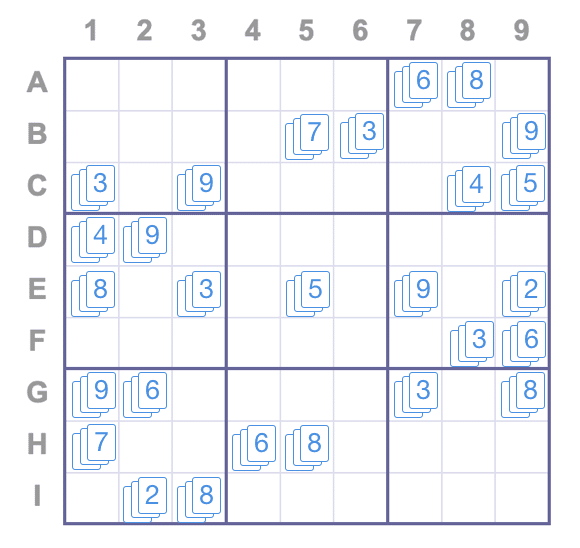
2) Successivamente, Alice codifica la sua soluzione facendo in modo che la macchina disponga le sue risposte a faccia in giù sulla griglia. Ovviamente, la macchina impedisce a Bob di capovolgere le carte nelle loro celle.

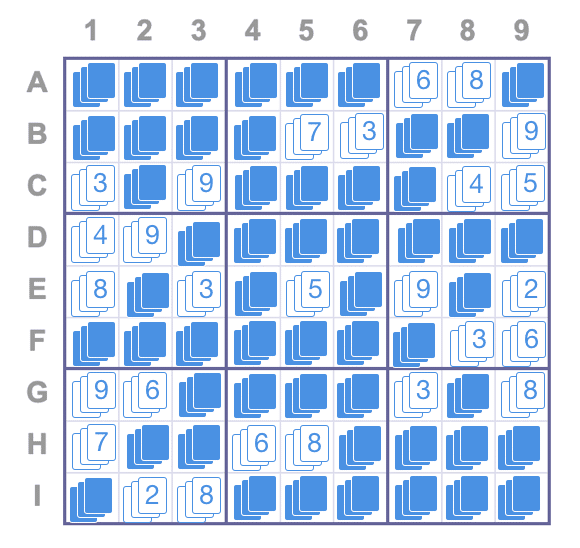
3) Ora Bob può interagire con la macchina. A partire da ogni riga, Bob sceglie casualmente una carta in ogni cella, dall’alto, dal centro o dal basso.

(Bob raggruppa le carte per la riga 1)

La macchina prende le carte scelte e assembla un pacchetto a faccia in giù da 9 carte per ogni riga.

Questa azione viene ripetuta anche per ogni colonna. Infine, le carte rimanenti vengono ordinate in un unico pacchetto per ogni griglia 3×3. In totale, la macchina produce 27 pacchetti.

4) Poi la macchina mescola casualmente le carte di ogni pacchetto, prima di restituire i pacchetti a Bob.

5) Bob scopre le carte e verifica che ogni pacchetto contenga i numeri da 1 a 9, senza numeri mancanti o duplicati.

(Le carte sono state mescolate e non hanno più l’ordine originale)

Dopo qualche giro di verifica, Bob e gli amici sono convinti che Alice ha risolto questo rompicapo.

In questo esempio, la dimostrazione non è interattiva. Chiunque può utilizzare la macchina (o in realtà il codice) per verificare la rivendicazione di Alice. Alice non deve essere presente per esser messa alla prova.

Ecco qua! Per una panoramica più completa, controlla il podcast ZeroKnowledgeFM.